Simulating the Effects of Artificial Gravity
The most commonly considered method of artificially simulating gravity in space is by using a constantly rotating frame. This form of artificial gravity carries with it some issues related to the physics of rotating frames. The main two effects of concern are that of the Coriolis Effect, and the Centrifugal Force Gradient.
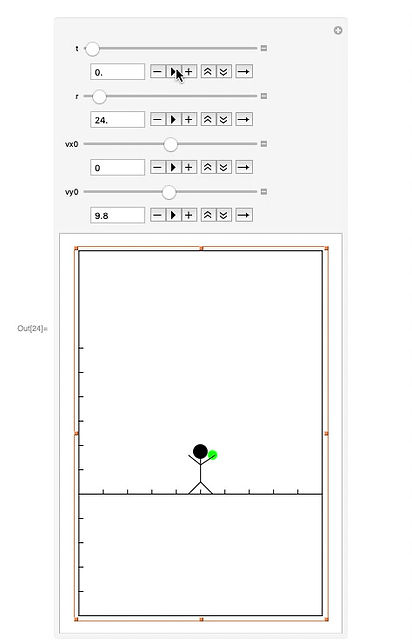
The Coriolis Effect bends moving objects in a direction perpendicular to their trajectories, resulting in bizarre curving of objects. This can be seen in the animation to the left, which I created from scratch using Mathematica. This applet can show the trajectory of a dropped/thrown ball (green circle) inside an "artificial gravity" chamber for a variety of chamber sizes (r parameter is radius of cylindrical chamber), and for different initial velocities of the ball.
Also, due to the fact that centrifugal force depends on distance from the center axis of rotation, the artificial gravitational force would be less strong on the astronaut's head than their feet when standing up. This "gravity gradient" may have negative physiological effects on astronauts.
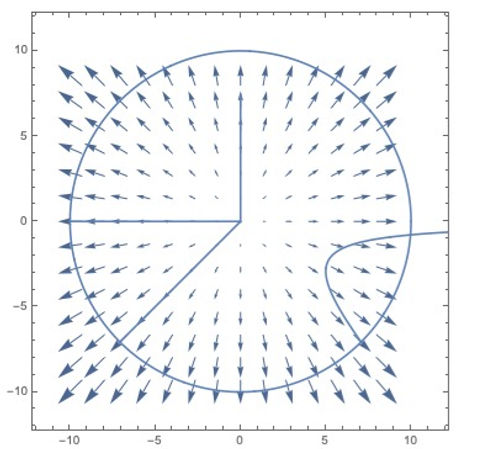
Centrifugal Force Gradient
This vector plot demonstrates the centrifugal force gradient of a cylindrical section of a space station. As you can see, the force is stronger as you move outward, and is nonexistent at the very center of the rotation. The four lines are different trajectories--the two on the left are trajectories of objects that started just slightly off from center--they eventually accelerated to the outside. The vertical line is that of an object that was thrown from the edge of the compartment toward the center. It had the exact right initial velocity and direction to stop perfectly in the middle, and float there! (This is of course ignoring any air resistance and the Coriolis Effect). The parabola on the lower right is that of an object that was thrown vertically but with a slight horizontal component--it falls in a very similar fashion to true gravity, but with a slightly different path due to the force gradient.

